
Italian Pietro Mengoli was born in 1625 in Bologna. Mengoli received two Ph.D.s in the University of Bologna, Italy: one in philosophy in 1650, and the second in civil and canon law in 1653. After Cavalieri’s death, Pietro’s mathematics professor, Mengoli became chair of the University of Bologna, as well as a parish priest in Bologna. Although Mengoli had many disciplines, including astronomy, he studied mathematics with Cavalieri, and his studies resulted in his recognition in mathematics for discovering proofs on infinite series forty years before Johann Bernoulli.
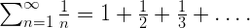
Mengoli begins with the summation of geometric series in his book Novae quadraturae arithmeticae, seu de additione fractionum published in 1650. He then showed that “the harmonic series does not converge. In doing so he became the first person to prove that it was possible for a series whose terms tend to zero to be made larger than any given number” (JJ O’Connor & EF Robertson. Para. 4). In other words, the series diverges to an infinite amount. Another one of his investigations resulted in proving that the summation of the alternating harmonic series is equal to, or better said, “converges to” the natural logarithm of 2. So, even though Mengoli wasn’t greatly acknowledged by the public, he was still the first one to prove that the harmonic series diverges; and he proved a few more infinite series.

Pietro also published a second book in 1659 called Geometriae Speciosae Elementa. This book was based on a theory of limits in geometrical figures, and “it contained a definition of a definite integral in terms of the area of a plane figure rigorously given by constructing and inscribing parallelograms which sum to equal limits”; three decades before Newton and Leibniz, “Mengoli was setting up the basic rules for calculus” (O’Connor & Robertson, para. 9). Both Newton and Leibniz were influenced by Mengoli’s work, either directly or indirectly, which is the reason why Mengoli is acknowledged.
His few books that Mengoli published were only known to Collins, Leibniz, and Wallis. Pietro’s recognition “lies in the transitional position of his mathematics, midway between Cavalier’s method of indivisbles and Newton’s fluxions and Leibniz’ differentials” (O’Connor & Robertson, para. 8). In other words, Mengoli’s studies in calculus and infinite series established some groundwork for Newton and Leibniz to advance in their insightful ideas in calculus. Pietro Mengoli continues to be investigated, and he also contributed in other fields of science, such as astronomy. His Italian written books may also have contributed to the lack of acknowledgment that the math community had given Megoli; either way, we still know him as one of the first mathematicians that proof that the harmonic series diverges to infinity.
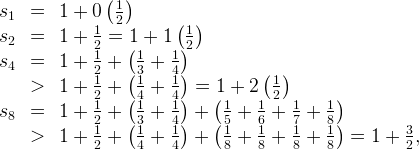
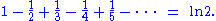






 RSS Feed
RSS Feed